🎄🧑‍💻 Day 5: Hydrothermal Venture

Sun, 5 Dec 2021

Go here to read Day 5's puzzle text in full.

Day 5's problem happens to be similar to last year's Day 3 problem. I must say that I found 2021s puzzle much easier than 2020s, restating the words of Advent of Code's creator: the difficulty of puzzles “is not meant to be a perfect monotonically increasing sequence.” Difficulty depends on a lot of factors, many of which are personal.

The only concept required is a basic understanding of Cartesian coordinates, and the solution to the second part implied a simple reasoning based on symmetry. But let's start from the beginning.

Part 1

I'll use a simpler example to describe my solution: instead of using a 10 x 10 grid, I'll use a 5 x 5 one. Without loss of generality, mathematicians like to say.

The (simplified) input is a list of coordinates representing segments (or vectors) on our grid. In short, the first question asks to count how many times a cell in the grid is being crossed by at least two segments. We then have to keep track in which cells each segment starts and ends, including every cell it goes through. Last bit of information: we should ignore diagonal segments.

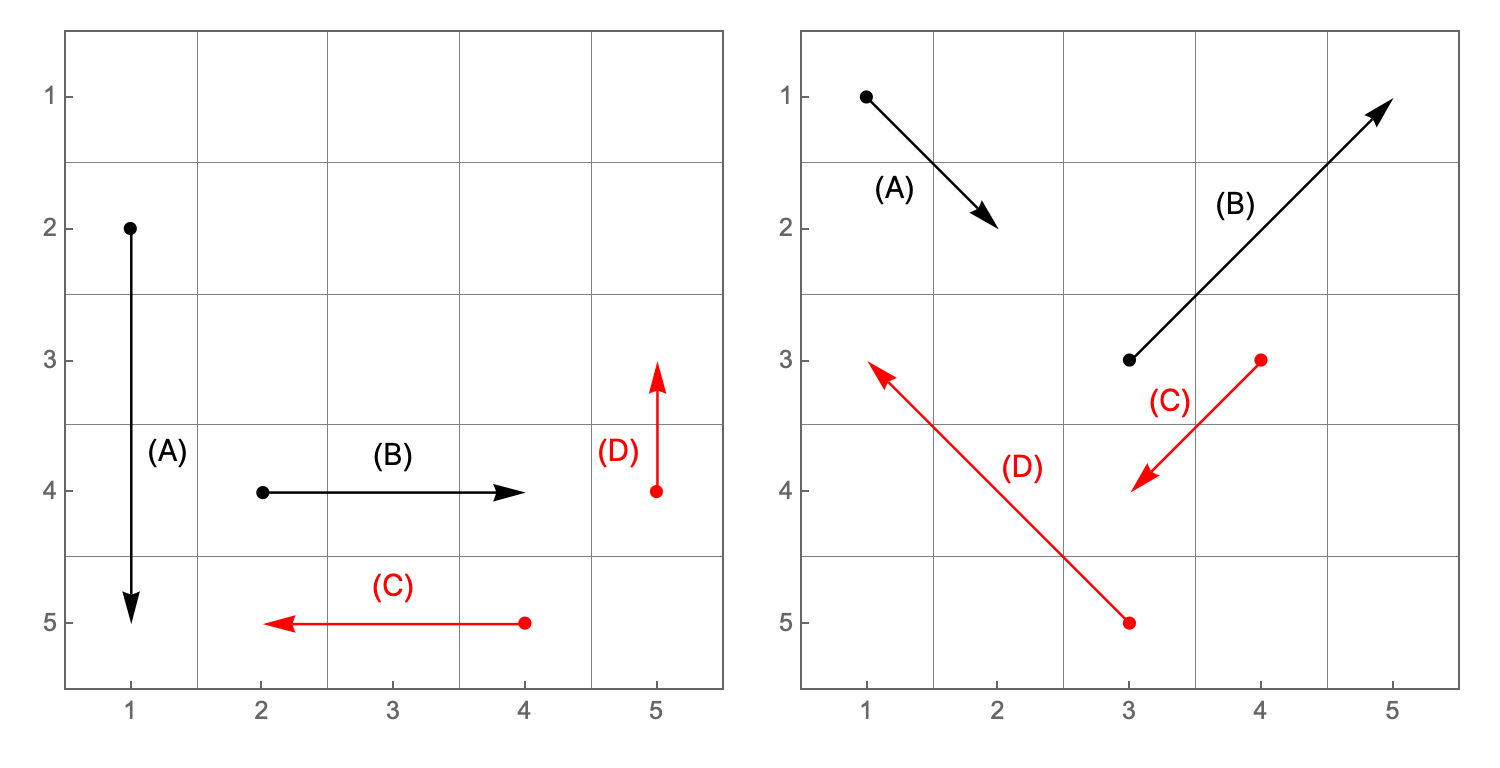
Consider the following 4 segments:

A: (1,2) → (1,5)
B: (2,3) → (4,3)
C: (4,5) → (2,5)
D: (5,4) → (5,3)

On each line, the first is point 0 (x_0,y_0) and the second is point 1 (x_1,y_1).

Start by creating a blank grid, a 5 x 5 matrix (list of lists) filled with zeroes:

grid = [[0 for _ in range(5)] for _ in range(5)]

We can mark all the cells that are touched by those segments with two for loops, each of which considers separately the case of horizontal (constant y coordinate) or vertical (constant x) segments:

if x_0 == x_1:
	for i in range(y_1 - y_0 + 1):
		grid[x_0][y_0 + i] += 1

if y_0 == y_1:
	for i in range(x_1 - x_0 + 1):
		grid[x_0 + i][y_0] += 1

This code will handle correctly the two black segments of the figure above (left side). What about the red ones? The code doesn't know (yet) what to do with negative segments, whose endpoints are closer to the origin than the starting points. The point is (pun intended): we don't care about the direction of the segments, only their lengths (how many cells they cross). For negative segments, we can swap the coordinates.

if x_0 == x_1:
	if y_1 < y_0:
		y_0, y_1 = y_1, y_0
	for i in range(y_1 - y_0 + 1):
		grid[x_0][y_0 + i] += 1

if y_0 == y_1:
	if x_1 < x_0:
		x_0, x_1 = x_1, x_0
	for i in range(x_1 - x_0 + 1):
		grid[x_0 + i][y_0] += 1

To obtain the answer to the question “At how many points do at least two lines overlap?”, we need four more lines of code:

unroll = []
for r in grid:
	unroll.extend(r)
	
# Part 1 answer
print(len(list(filter(lambda x: x >= 2, [_ for _ in unroll]))))

The most interesting bit of the code above is the last line, but you guessed: it keeps only elements greater than or equal to 2 with filter, and then count the items left with len.

Part 2

As expected, we must now include diagonal segments, but fortunately only those at 45 degrees, that is, increments will be identical in X and Y directions.

The rightmost figure above has 4 diagonal segments, and we can apply the same argument for “negative segments” along X or Y. We need to invert the direction of the two red segments so that we can treat them as the black ones.

Both red segments have x_1 < x_0, and the block of code to add to deal with diagonal segments is

if x_1 < x_0:
	x_0, x_1 = x_1, x_0
	y_0, y_1 = y_1, y_0
	
if y_1 < y_0:
	for idx in range(x_1 - x_0 + 1):
		grid[x_0 + idx][y_0 - idx] += 1
else:
	for idx in range(x_1 - x_0 + 1):
		grid[x_0 + idx][y_0 + idx] += 1

If y_0 > y_1, the Y coordinate must be decremented, otherwise incremented as the X. Why? Look at the segment labeled "C" in the right panel of the figure above. If you flip its direction, you'll see that y now must go from 4 to 3.

A Wolfram approach

Another way to approach the problem is the following. From the list of start and end points coordinates, build another list with the coordinates of all the points in between. For example, from (0,9) → (5,9) obtain the list {{0, 9}, {1, 9}, {2, 9}, {3, 9}, {4, 9}, {5, 9}}. If we have a list like that for every pair of coordinates, then we can recursively update the grid for each of these “update points”.

The main piece of code is the function that builds the intermediate points from a pair of coordinates. Here's my idea¹, but I'm sure it can be improved:

range[{x0_, y0_}, {x1_, y1_}] :=
 
Transpose @ {
   
   Which[
       x1 < x0, Range[x0, x1, -1],
       x1 == x0, ConstantArray[x0, Abs[y1 - y0] + 1],
       True, Range[x0, x1]],
   
   Which[
       y1 < y0, Range[y0, y1, -1],
       y1 == y0, ConstantArray[y0, Abs[x1 - x0] + 1],
       True, Range[y0, y1]]
}

With that function, we can build the full list of grid points to update:

updates = Reverse /@ Flatten[Map[Apply[range], points], 1]

A comment on Reverse is worth: as the grid is a matrix, {x, y} means “row x and column y”, but the puzzle's text considers a Cartesian system where the x moves along the columns of the grid matrix, and y along the rows. That's why we have to swap them, but only if we want to obtain an identical visual representation. The absolute location of a grid cell doesn't matter, only if it has been crossed more than twice.

Here's the last bit of Wolfram code: updating the grid for each of the update points.

finalGrid = Fold[MapAt[(# + 1) &, #1, #2 + 1] &, grid, updates]

Fold takes three arguments — a function, a starting value, and a list — and returns the last element of the list of recursive applications of the function: Fold[f, x, {a,b,c}] = f[f[f[x, a], b], c]. In the line above, the function is MapAt, that adds 1 to the grid (argument slot #1) at a given position (#2); the #2 + 1 accounts for list indexes starting at 1 instead of 0.

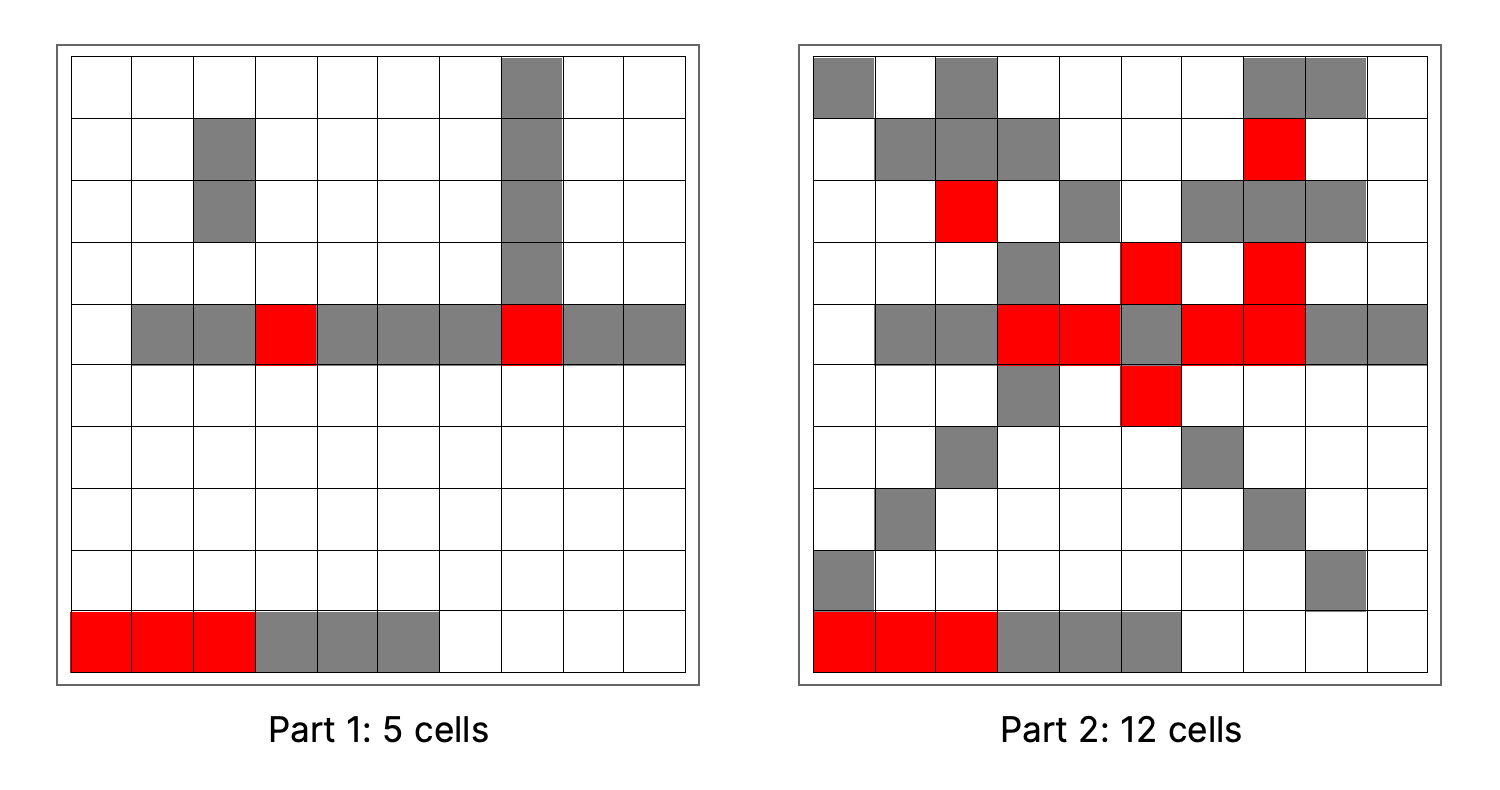
For a small example, we can visually determine the answer to both parts:

#advent of code #programming #python #wolfram